Time-parallel methods address the question of what to do when one has reached the limits of strong scaling (decreasing wall-clock time by increasing the number of processors working in parallel) through domain decomposition parallelisation in space. A milestone in the history of parallel-in-time algorithms is the Parareal algorithm (Maday and Turinici, 2002). In Parareal, successive time intervals are solved forwards in parallel. An iterative procedure is used to determine initial conditions for these time intervals, facilitated by a cheap but less accurate “coarse propagator” that is implemented sequentially. However, Parareal is not the only time-parallel algorithm, and there has been an explosion of parallel-in-time algorithms appearing in the literature in the last five years. A key lesson from the recent literature is that the success of parallel-in-time algorithms critically depends on them being carefully adapted to the PDE being solved. Much like regular time-stepping methods for PDEs, there are many parallel-in-time algorithms, and the right algorithm needs to be designed and selected according to the mathematical properties and applications requirements of the PDE. This calls for a design cycle from mathematics to computational science to applications science and back again; this is what our unique team provides.
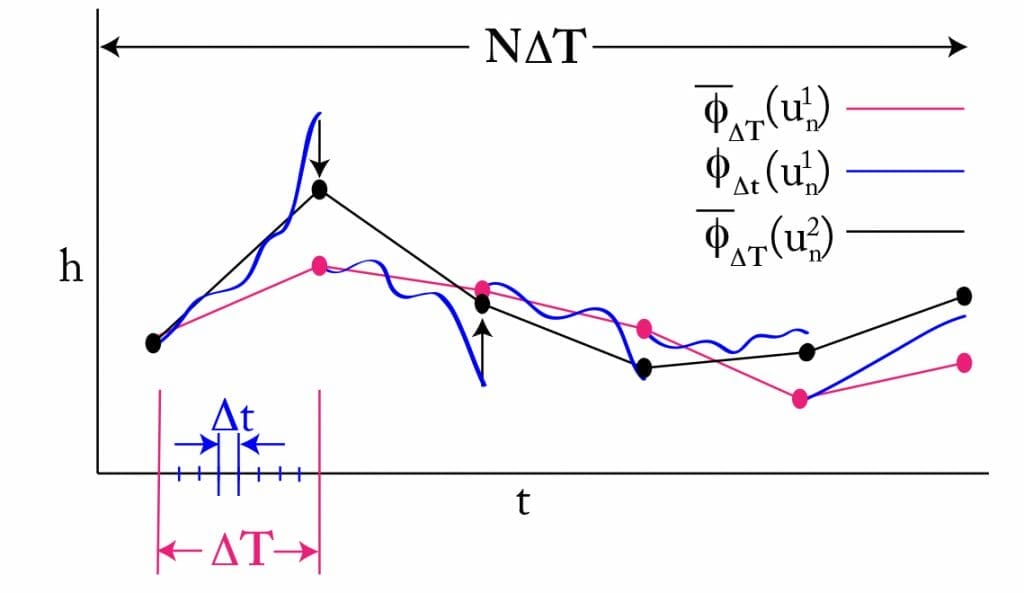
There are many results in the literature regarding the convergence and efficiency of parallel-in-time algorithms for specific, simple problems. There is also a wealth of practical experience that suggests these algorithms can deliver extensive speedups, even in complex simulations where their convergence properties are not yet fully understood.
Despite this wide range of successes, time-parallel methods have yet to impact model performance in operational settings because of three insurmountable barriers:
- Many operational scientific codes, built on standard scientific computing practices of the past, have hard-coded time stepping algorithms, making even simple changes monumental tasks;
- Parallel-in-time algorithms rely on complicated message passing interface (MPI) communication patterns that pervade the entire software stack from the outer time loop to e.g., model-specific preconditioners for linear systems; and
- Since there are many flavours of time-parallelism, the best one to use depends on the underpinning mathematical structure of the equations each with their own potential for practical implementation and parallel requirements. It is insufficient to provide a generic library for parallel-in-time algorithms where the specific model is plugged in as a black box, because changes to the model pervade the code at all levels in a performant implementation.
We will overcome these barriers by:
- Designing and implementing cutting-edge algorithms in an environment that allows for rapid prototypes based on contemporary scientific computing practices of ‘separation of concerns’, using domain specific languages and compilers, and inheritance and template metaprogramming. This will enable model specific algorithm choices at all levels of the code, from multigrid smoothers and transfer operators to vectorisation.
- Enabling RSEs and HPC research access to cutting edge algorithms to advance their deployment on current and future computing platforms.
- Opening the door to the next generation of time-parallel algorithms, as is expected from the large increase in the number of research papers on the subject over the last 10 years.
- Fostering creativity between mathematicians and RSEs (almost entirely absent in time-parallel methodologies due to these barriers) to find optimal, practical time-parallel solutions for some of our most pressing scientific problems. The legacy of such an activity could have impacts for decades into the future by enabling impactful research projects for computational scientists, mathematicians and application scientists, and for launching UK’s flagship scientific endeavours, such as those of the Met Office and UKAEA, to be at the forefront of Computational Science worldwide.
The project repository can be found here: https://github.com/jshipton/APinTA_testcases


